Causal Dynamic Networks : ODE Network Modeling of fMRI
Xi (Rossi) LUO
Department of Biostatistics
Center for Statistical Sciences
Computation in Brain and Mind
Brown Institute for Brain Science
Brown Data Science Initiative
ABCD Research Group

December 16, 2018
Funding: NIH R01EB022911, P20GM103645, P01AA019072, P30AI042853; NSF/DMS (BD2K) 1557467
Co-Authors

Xuefei Cao
Brown Applied Math

Björn Sandstede
Brown Applied Math
Slides viewable on web:
bit.ly /cmstat18
fMRI Experiments
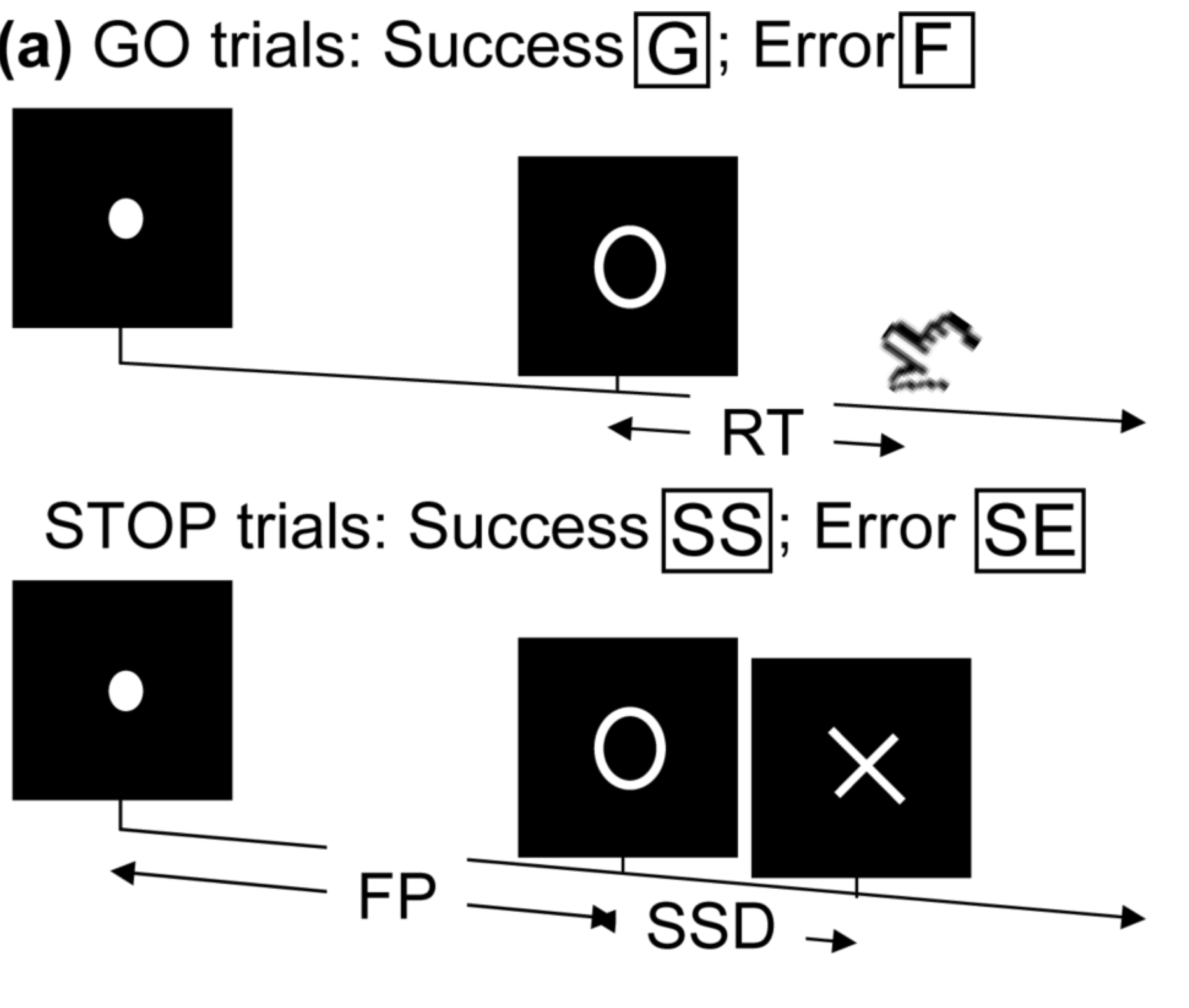
- Task fMRI: performs tasks under brain scanning
-
Randomized stop/go task:- press button if "go";
- withhold pressing if "stop"
- Resting-state: "do nothing" during scanning
fMRI data: blood-oxygen-level dependent (BOLD) signals from each
Conceptual Model with Stimulus

Sci Goal: infer intrinsic connections,
Some Existing Methods and Limitions
- Functional (nondirectional) connectivity:
- Correlations
- PCA, independent component analysis (ICA) Calhoun, Guo, and colleagues
- Graphical models (inverse covariance)
- Bayesian methods Bownman, Guindani, Vannucci, Zhang, and colleagues
- Effective (directional) connectivity:
- Granger causality, autoregressive modelsDing, Hu, Ombao, and colleagues
- Structural equation models
- Limitations:biophysical interpretability $\propto$ scalability${}^{-1}$
- Fail to model task-depend connections/activations
- Connections unlikely to be causal/neuronal
- Some are hard to scale to large networks
Dynamic Causal Modeling (DCM)
- Proposed by Friston et al, 2003 (> 3000 citations)
- System approach to address previous limitations:
- Latent neuronal states: a
network ODE model - From neuronal states to observed BOLD signals: another ODE
- (Bayesian) priors for model parameters
- Bayes factors for comparing
a few candidate models
- Latent neuronal states: a
- DCM essentially unchanged for the past 15 yrs Friston et al, 17


DCM: Advantages and Limitations
- Advantages:
Task -dependent,directional connectionsNeuronal/causal connections- Model brain activations (and non-stationary time series)
- Limitations:
- Computationally expensive
- Bayesian model comparison over exponentially many models
- Model performance depends on priors Frassle et al, 15
- Hard to scale (~10 nodes), some successes for simplified models
- Mostly for hypothesis validation, not
data driven
Our CDN Model and Method
Causal Dynamic Networks
- A two-level model
- 1. DCM neuronal state model (latent $\bm{x}$, stimulus $\bm{u}$): $$\frac{d\bm{x}(t)}{dt}=\bm{A}\bm{x}(t)+\sum_{j}u_j(t)\bm{B_j}\bm{x}(t)+\bm{C}\bm{u}(t)$$
- 2. BOLD data model (data $\bm{y}$, noise $\bm{\epsilon}$) at discrete $t_i$: $$ \bm{y}(t_i) =\int h(s)\bm{x}(t_i-s) ds + \bm{\epsilon} (t_i) $$
- $h$ hemodynamic response function
- $\bm{A}$ intrinsic connection matrix, $\bm{B}$ task-dependent connection tensor, $\bm{C}$ stimulus activation matrix
Functional/Dynamic Data Analysis
- Usually, observed data model $$ y(t) = x(t) + \epsilon(t) $$ and latent $x(t)$ follows an ODE model of interest
- Various approaches for estimating the ODE parameters: nonlinear least squares Xue, Miao, Wu, 10, two-stage smoothing Varah, 82, principal differential analysis Ramsey, 96, Bayesian Girolami, 08, EcoG Zhang et al, 15
- The observed data model not applicable to fMRI
- For example, two-stage smoothing approaches not directly applicable to BOLD
convolutions : $$ y(t) = \int x(t-u)h(u) du + \epsilon(t) $$
Hemodynamic Response Function (HRF)



fMRI responses last long (~30 seconds) after neural activities
"Smooth" BOLD far from neuronal activity
Method
- An optimization-based approach
- Minimize the following \[\begin{multline*} \scriptstyle l(\bm{x},\bm{\theta})=\sum_{t_i} \| \bm{y}(t_i)-h \star \bm{x}(t_i)) \|^2 \\ \scriptstyle +\lambda\int \left \| \frac{d \bm{x} (t) } {dt} - (A \bm{x}(t)+\sum_{j} u_j(t) \bm{B_j} \bm{x}(t)+ \bm{C}\bm{u}(t)) \right\|^2 dt \end{multline*} \]
- Balancing data fitting errors and ODE fitting errors
- Plug in basis-expansion of $\bm{x}(t) = \bm{\Gamma} \bm{\Phi}(t)$
- Allows convolution (vs two-stage smooth approach)
- Computationally fast to allow Bootstrap
inference
Algorithm
- Prove conditional convexity of $O(J d^2)$ parameters
- Iterative block coordinate descent algorithm
- Prove explicit update formulas (no numerical optimization algorithms needed)
Special Case: Resting-state fMRI
- Set our parameter $\bm{B}$ and $\bm{C}$ to zero
- Only fit intrinsic connection $\bm{A}$
- Can fit much larger networks
Simulations
Simulation: vs GCA/VAR

Our
Simulation: vs DCM

Our
Uncovering Neuronal States

Decent recovery of (latent) neuronal states
Task fMRI and Resting-state fMRI
Stop/Go fMRI

Brain activations and instrinsic connections between regions
Task Specific Connections

"Go" connections

"Stop" connections
Better understanding of brain mechanisms
Resting-state Connections

Ours (A) close to DCM (C), different from correaltions (B)
Real Data: 264 Brain Regions

CDN uncovers a
Discussion
- Joint optimization method for infer ODE networks
- Flexible models for observations from causal ODEs
- Computationally efficient for large-scale modeling
- PyPI pacakge:
cdn-fmri
Thank you!
Comments? Questions?
BigComplexData.com
or BrainDataScience.com