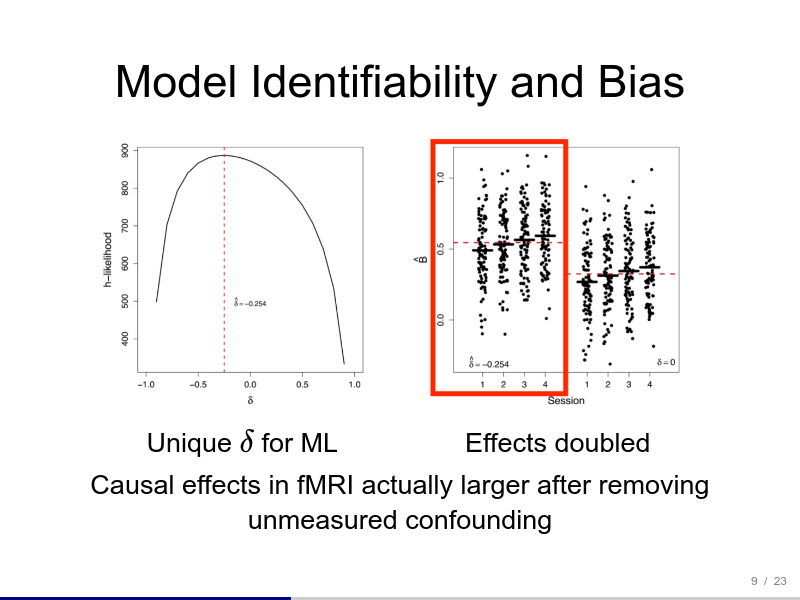
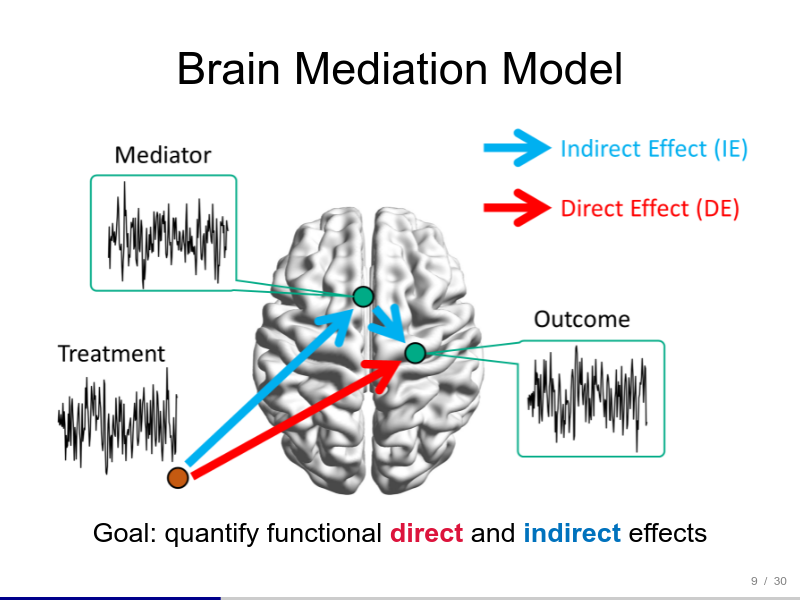
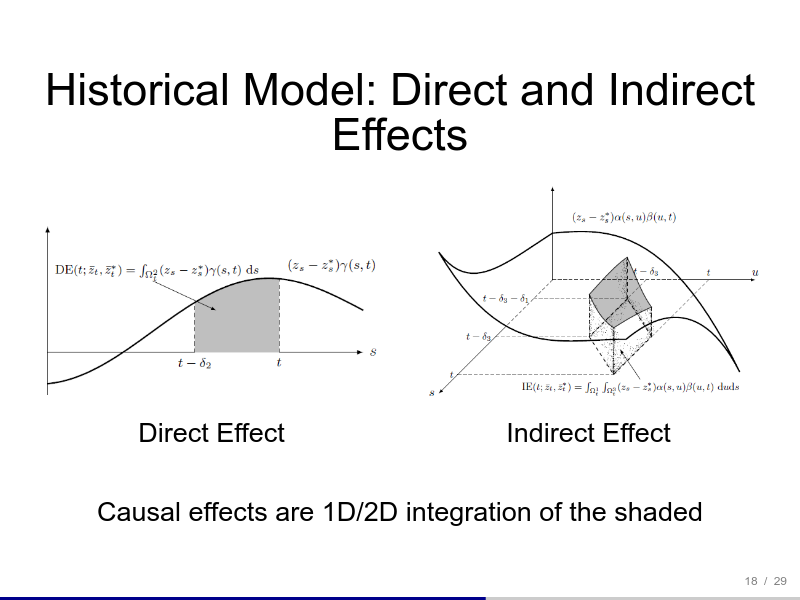
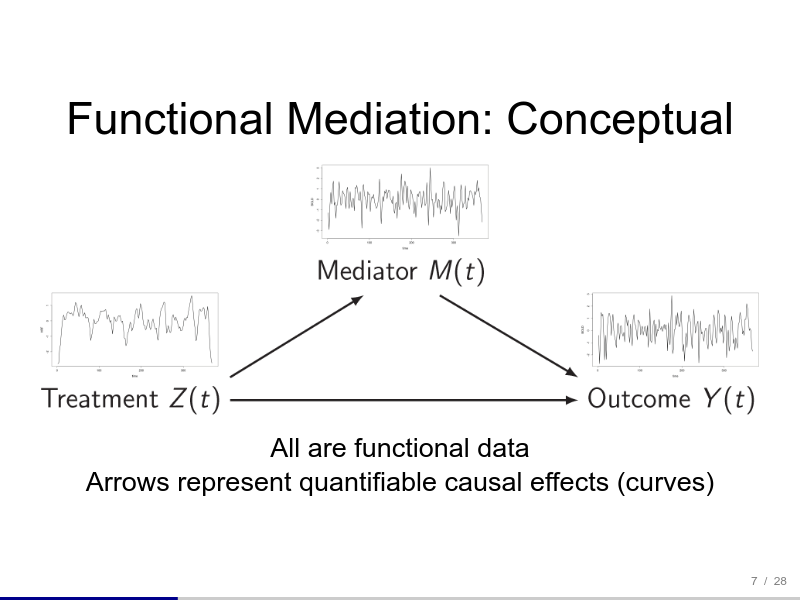
Talks
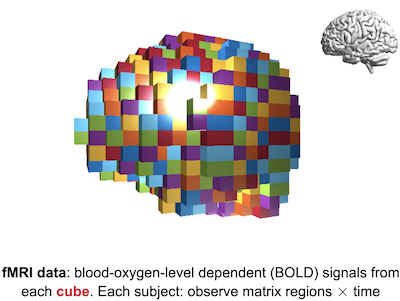
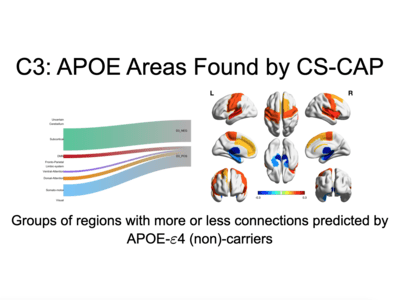
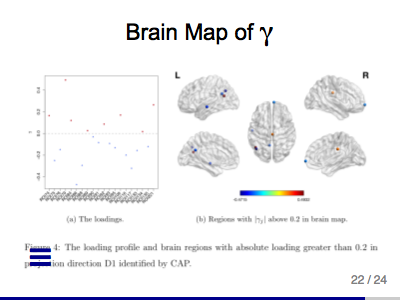
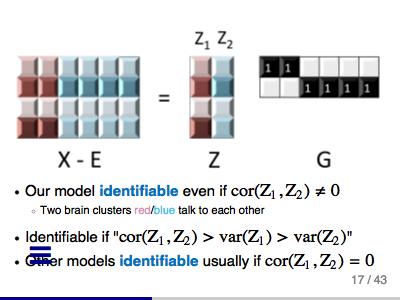
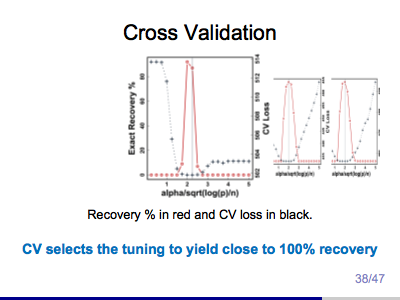
Covariance Outcome Modelling via Covariate Assisted Principal (CAP) Regression
On August 1, 2023 at EcoSta 2023
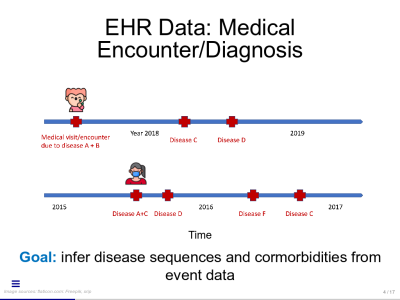
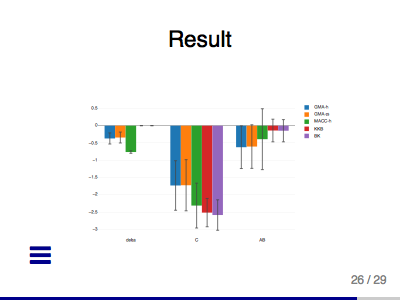
Binary Autoregressive Network Modeling of Comorbidity Networks from Electronic Health Records
On December 15, 2020 at ICSA 2020
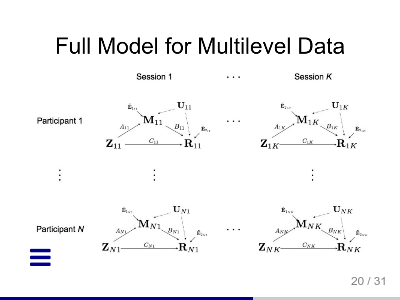
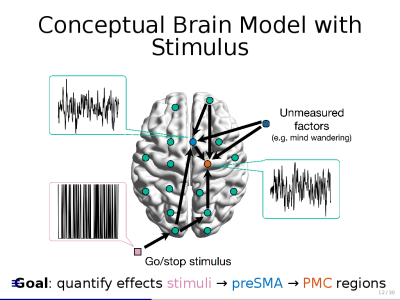
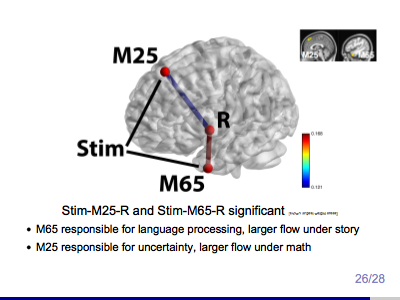
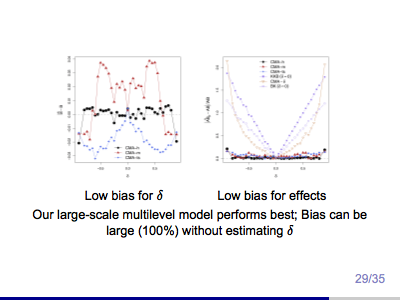
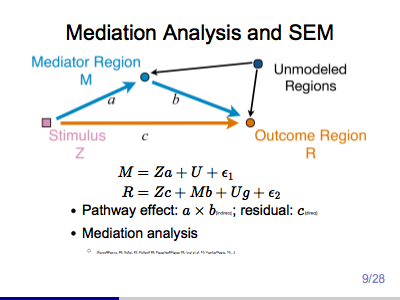
Estimating Brain Pathway Effects Using Large-scale Multilevel Models
On June 25, 2017 at 2017 ICSA Symposium
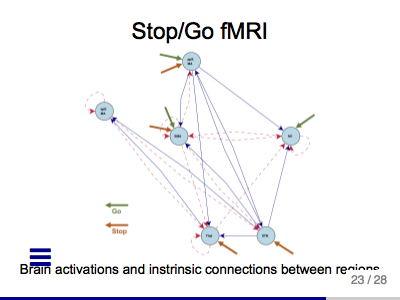
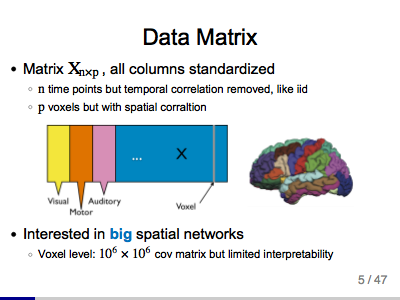
Network Clustering with an Application to fMRI
On June 16, 2017 at EcoSta Conference HKUST Business School
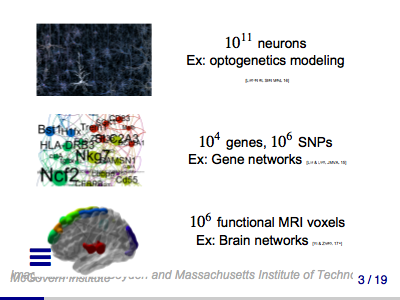
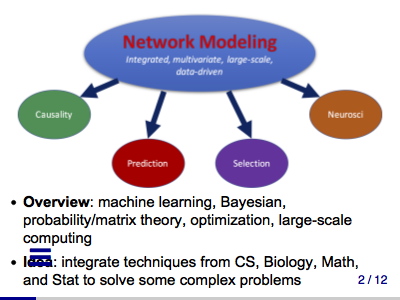
From Big Data to Knowledge: Brain, Twitter, and Beyond
On April 19, 2017 at Brown A Day on College Hill
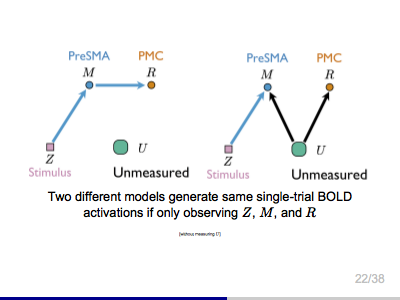
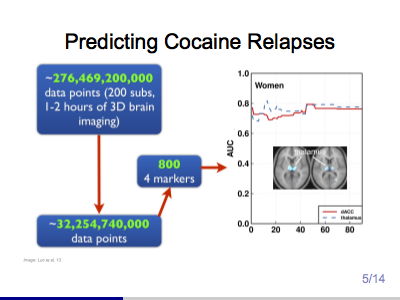
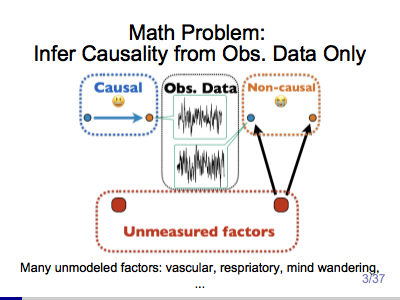
Big Complex Data, Causality, and Brain Pathways
On December 27, 2016 at Big Data and Medical Imaging
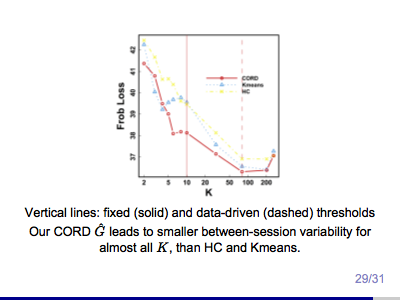
Network Communities and Variable Clustering via CORD
On June 7, 2016 at Statistical Learning and Data Science
From Big Data to Knowledge: Brain, Twitter, and Beyond
On April 20, 2016 at Brown A Day on College Hill
Graphical Models for Brain Connectivity: Algebraic (Non-likelihood) Methods
On February 23, 2016 at SAMSI Working Group